自作移動ロボットのハードウェア構成


はじめに

　前回の記事冒頭でも言及した通り、図1に示す移動ロボットを自作して遊んでいます。今回は、この機体のハードウェア構成を雑に紹介します。たまにソフトウェアの話も混ざっていますが気にしないでください。

 

図1　自作移動ロボット

 

全体構造

　図1を見ると分かる通り、3段のアクリル板に各部品をねじ止めした構造です。アクリル板同士は六角スペーサで固定しています。アクリル板の形状とねじ穴の配置は、Fusion360で設計しています。

 

電装部品の構成

　自作移動ロボットには、自律走行・SLAM・センサフュージョン等をして遊ぶために、様々な電装部品を搭載しています。図2に接続構成の概要を示します。

 

図2　電装部品接続構成の概要

 

　電装部品の核となるのは、Minisforum社製のミニPCであるUN305Cです。このPCにUbuntu22.04をインストールした上で、ROS 2 Humbleの環境を構築しています。USB PD給電で動作可能であること、低消費電力の割に性能の良いi3-N305プロセッサを搭載していることから選定しました。

　また、GNSS・LiDAR・6軸（加速度と角速度）・地磁気・気圧の各センサを搭載しています。GNSSとLiDARは既製品のモジュールをUSBケーブルでミニPCに接続しています。残りのセンサは自作のセンサ基板に搭載した上で、USBケーブルでミニPCに接続しています。どのセンサとも、ミニPCへUSBシリアル通信を用いてデータを送信し、ミニPC上で受信ノードを走らせROSトピックをpublishしています。

　走行のためのアクチュエータとしては、2個のエンコーダ付きギアモータを搭載しています。自作のモータ制御基板がミニPCから回転数指令を受け取り、既製品のモータドライバに対して電圧指令をPWM信号にて送信する構成です。モータ制御基板も、ミニPCへUSBシリアル通信を用いてモータ角度・角速度等のデータを送信し、ミニPC上で受信ノードを走らせROSトピックをpublishしています。

 

下段アクリル板の構成

　ここからは、3枚ある各アクリル板ごとに紹介していきます。図3に、下段アクリル板に搭載した部品を示します。

　まず、足回りから紹介します。左右1つずつの動輪と1つの自在キャスターから構成された、差動二輪方式を採用しています。以前は受動輪としてボールキャスターを使用していましたが、屋外を走行すると異物が挟まりやすかったため、自在キャスターに変更しました。

　また、以前はタイヤとして、後述するエンコーダ付きギアモータと同じPololu製の物を使用していました。しかし、幅が小さくちょっとした隙間にはまり込んでしまうため、3Dプリントの自作タイヤに変更しました。白色部はレジン、黒色部はTPUで製作しています。

 

図3　下段アクリル板と部品

 

　タイヤの取り付け方法にも少しこだわっています。イモネジは緩みやすいので使いたくありません。図4の様に、端面にねじ穴が開いているセットカラーをモータ軸に取り付けた上で、ねじ穴に3Dプリントタイヤを固定しています。

　エンコーダ付きギアモータには、Pololu製の"100:1 Metal Gearmotor 37Dx73L mm 12V with 64 CPR Encoder (Helical Pinion)"を使用しています。ギア比は約100:1で、四逓倍した上で1回転64パルスのエンコーダが付属しています。よって、出力軸において約0.055°の分解能で角度を計測できます。

図4　エンコーダ付きギアモータと3Dプリントタイヤ

 

　モバイルバッテリーとミニPCも下段アクリル板に搭載しています。重量が大きいこれらの部品を下部に搭載することで、低重心化を図っています。

 

中段アクリル板の構成

　中段には、図5の様に、主に基板と上段に載せる必要がないセンサ類を搭載しています。

 

図5　中段アクリル板と部品

 

　センサ基板には、図6の様に6軸センサ・地磁気センサ・気圧センサを搭載し、マイコンとしてSTM32F446REを搭載しています。加速度・角速度・地磁気センサを用いてロボットの姿勢角を計算し、ミニPCへ送信することがこの基板の主な役割です。なお地磁気センサは、前回の記事で紹介したアルゴリズムを用いた初期姿勢角の算出のみに用いています。その後は、加速度・角速度センサ値のみを用いたカルマンフィルタで姿勢角を計算しています。

　STM32F446REは動作クロック180 MHz、FLASHは512 KB、RAMは128 KBとそれなりにリッチなマイコンであるため、数値計算ライブラリEigenを用いてカルマンフィルタを実装しても、Releaseモードでビルドすれば問題なく更新周期0.01秒で計算できています。

　気圧センサは、気圧高度・GNSS高度・ピッチ角と車輪速を組み合わせて高度を算出すると面白いかなと思って搭載していますが、まだ活用できていません。

 

図6　センサ基板

 

　図7に示すモータ制御基板は、エンコーダ付きギアモータの回転数制御と、そのデータをミニPCへ送信することが主な役割です。回転数制御の機能は、ミニPCから指令を受け取るモードと、図8に示すコントローラーから指令を受け取るモードの2モードを備えています。

　コントローラーとモータ制御基板の双方には2.4 GHz帯無線マイコンであるTWE-LITEを搭載しており、ラジコン操作を可能としています。手動走行したい場合に、この機能を用いています。

 

図7　モータ制御基板

 

図8　コントローラー

 

上段アクリル板の構成

　上段には、図6の様に2D LiDARとGNSSセンサを搭載しています。GNSSアンテナの高さは、2D LiDARがスキャンする面より低くなっており、全周をスキャンできるようにしています。

 

図9　上段アクリル板と部品

 

　2D LiDARにはYDLIDAR X4 PROを使用しています。約1万円と比較的安価に購入でき、公式にROS 2ドライバが配布されていたことが採用理由です。家の中でROS 2のslam_toolboxを使って遊ぶには十分な性能です。ただし、回転部の軸と重心がかなりずれているようで、振動が発生する点が難点です。

 

　GNSSセンサには、Ublox社のNEO-F9PとNEO-D9Cを用いています。この2つのチップは組み合わせて用いることで、いわゆる「日本版GPS」みちびきのセンチメータ級測位補強サービスCLASを活用可能です。オープンスカイの環境であれば、誤差数センチメートル以内の測位結果が得られます。

　2つを組み合わせて使用することを前提として設計されている、ジオセンス社のモジュールを購入して搭載しています。合計で5万円しますが、CLAS対応GNSSモジュールの中では安価と思います。

ZED-F9P RTKシステム開発用ボード F9PX1 : ジオセンス ヤフー店 - 通販 - Yahoo!ショッピング

みちびき CLAS L6受信用 NEO-D9C開発ボード D9CX1 : ジオセンス ヤフー店 - 通販 - Yahoo!ショッピング

 

　なお、2モジュールを組み合わせた上でCLASを使用する設定済み、かつアンテナも付属したセットが販売されています。価格は高くなりますが、手間は省けます。私は安いばら売りの方を買い、CLAS使用設定に手間取り1日かかりました。

 

store.shopping.yahoo.co.jp

 

　GNSSアンテナは、GPSに加えてCLAS使用に必要なみちびきの周波数帯を受信可能な物を搭載しています。アンテナの下にはグランドプレーンと呼ばれる金属板を配置しています。これは反射波の影響を低減し、測位精度低下を防ぐものです。もう少し大きい方が良いと思われますが、車体からはみ出すので今のサイズとしています。

 

自作部品の発注先

　センサ基板・モータ制御基板ともElecrowへ発注しています。部品実装サービスもありますが、使ったことはなく手はんだしています。

　アクリル板と3Dプリント部品も、主にElecrowへ発注しています。ただしタイヤだけは、TPUフィラメントの取り扱いがあるJLCPCBへ発注しました。

 

おわりに

　移動ロボットの自作は楽しいので、皆さんもぜひやってみてください。次回の記事では、このロボットに実装している、GNSS測位データ・車輪速データ・姿勢角データを組み合わせたカルマンフィルタによる位置推定を紹介する予定です。

地磁気センサ値を鉛直軸まわりの回転のみに用いた初期姿勢角算出方法


はじめに

　最近、図1左に示す移動ロボットを自作して遊んでいます。この機体に、図1右に示す3軸加速度、3軸角速度、3軸地磁気センサを備えた基板を搭載しています。

　この基板に、ロボットの姿勢角を計算するプログラムを実装しています。今回は、実装したプログラムにおいて使用している、初期姿勢角の算出アルゴリズムを紹介します。

　本アルゴリズムは、地磁気センサ値を鉛直軸まわりの回転算出のみに用い、傾きには影響しないようにしている点が特徴です。なお本記事では、特に言及のない限り計測誤差のない理想的な状態を仮定して議論します。

 

図1　自作移動ロボット(左)とセンサ基板(右)

 

座標系とクォータニオンの定義

　本記事中では、基準座標系をNWU（x軸が北方向、y軸が西方向、z軸が上方向）の局地座標系とします。

　また、本記事中では要素0が実部、要素1~3が虚部のクォータニオンを用いて回転を表します。つまり、単位ベクトル \boldsymbol{\eta}=[\eta_x\quad \eta_y\quad \eta_z]^{\mathrm{T}} を軸とした\theta [rad]の回転を表すクォータニオンqは、式(1)で表されます。

 

考え方

　クォータニオンq_rで表される基準座標系からセンサ座標系への回転を、図2のように2回にわたる回転q_mとq_gで表現することを考えます。このとき、クォータニオン積を * で表すと式(2)が成り立ちます。

図2　回転の順番

 


　なお、q_mは基準座標系のz軸周りの回転、q_gは基準座標系をq_mで回転させた中間座標系のx, y軸周りの回転とします。このとき、まず q_gを加速度センサ計測値から算出します。次に、地磁気センサ計測値とq_gを用いて中間座標系における地磁気の値\boldsymbol{m}_Iを算出し、それを用いてq_mを算出します。最後に、式(2)を用いてq_rを算出します。

 

中間座標系からセンサ座標系への回転の算出方法

　中間座標系は、基準座標系をz軸周りのみで回転させた座標系です。よって、この座標系における加速度の値\boldsymbol{a}_Iは式(3)で表されます。

 

 

　一方、センサ座標系における加速度センサ計測値\boldsymbol{a}_s=[a_x\quad a_y\quad a_z]^{\mathrm{T}}は、\boldsymbol{a}_Iにq_gを用いた座標系の回転をほどこした値です。よって、参考文献[1]に基づくと式(4)が成り立ちます。ただし、q_gはx, y 軸周りの回転であるため、q_3成分を0としています。

 

 

　式(4)とa_x^2+a_y^2+a_z^2=g^2 が成り立つことを用いると、q_gの各要素は式(5)または式(5)の各項の正負を反転した値と求まります。

 

 

　ただし、\boldsymbol{a}_s=[0\quad 0\quad -g]^{\mathrm{T}} つまりセンサが上下逆さまとなったとき、q_{g,1} と q_{g,2} の分母と分子がそれぞれ0となってしまいます。中間座標系のx軸とy軸どちらの軸周りであっても180度回転させれば上下逆さまとなることをイメージすれば分かりやすいですね。

　実装上は、a_z の値が -g に近い場合には式(5)で q_gを求めるのではなく q_g=[0\quad \frac{\sqrt{2}}{2}\quad\frac{\sqrt{2}}{2}\quad 0]^{\mathrm{T}} とする処理を追加すればよいでしょう。尤も、私のように移動ロボットに適用する場合は、逆さになることはないですが。

中間座標系における地磁気値の算出

　センサ座標系における地磁気センサ計測値 \boldsymbol{m}_s=[m_x\quad m_y\quad m_z]^{\mathrm{T}}に q_g の逆回転をほどこすと、中間座標系における地磁気値 \boldsymbol{m}_I=[m_{I,x}\quad m_{I,y}\quad m_{I,z}]^{\mathrm{T}} が求まります。

　q の共役クォータニオン q^*は q の逆回転を表すことを用い、式(6)により求めましょう。

 

 

基準座標系から中間座標系への回転の算出方法

　基準座標系における地磁気の値を \boldsymbol{m}_E=[m_n\quad m_w\quad m_u ]^{\mathrm{T}}とします。また、基準座標系から中間座標系への回転をz軸周りの\psi [rad] の回転とします。ただし、\psi の値域を -\pi\leq\psi\lt\pi と定義します。

　このとき、幾何学的関係により式(7)、(8)が成り立り、連立して解くと式(9)、(10)が求まります。

 

 


　ただし、m_n、m_wはそれぞれ地磁気の北方向成分、西方向成分です。国土地理院ホームページ[2]を用いると、日本列島周辺の指定した地点における地磁気の水平分力及び偏角が求まります。これらの値からm_n、m_wを計算するとよいでしょう。

　ここで、式(1)、(9)及び半角の公式により、基準座標系から中間座標系への回転を表すクォータニオン q_mについて式(11)が得られます。

 



　ただし、 -\pi\leq\psi\lt\pi の範囲では \cos\left(\frac{\psi}{2}\right)\geq 0 が成り立ちます。またその範囲では、\sin\psi と\sin\left(\frac{\psi}{2}\right)の正負は同一です。よって、q_mは式(12)により求まります。

 

 

基準座標系からセンサ座標系への回転の算出方法

　最後に、基準座標系からセンサ座標系への回転を表すクォータニオン q_r を求めます。

　式(5)により求めた q_g と、式(12)により求めた q_m を用いて、式(2)により求まります。実装においては、ロボットを静止させた状態で、加速度センサ値、地磁気センサ値各軸の平均値を取得した上で、算出に用いるとよいでしょう。


おわりに

　本記事では、3軸角速度、3軸地磁気センサ値を用いた初期姿勢角の算出方法を紹介しました。地磁気センサ値を鉛直軸まわりの回転算出のみに用いているため、地磁気センサの精度が低くとも傾きの算出には影響しません。ぜひ活用してみてください。

 

参考文献

[1] 矢田部学, クォータニオン計算便利ノート, MSS技報, 18巻, 2007

[2] 国土地理院, "地磁気値(2020.0年値)を求める", 国土地理院ホームページ, https://vldb.gsi.go.jp/sokuchi/geomag/menu_04/index.html, (参照 2025-6-8)

 

 

 

SONY製デジカメの液晶保護フィルムを剥がした

はじめに

　8年間使用しているSONY製デジタルカメラ「RX10M2」の液晶画面が、図1のようにガビガビになって困っています。ここまで傷がつくほど雑に扱った覚えはないのに......

 

図1　8年間使ったRX10M2の液晶画面

 

先行事例

　下記の先行事例を確認しました。SONYのカメラには購入時点からデフォルトで液晶保護層が施されていて、それが劣化するとガビガビになってしまうそうです。

　また、この劣化した保護層を剥がし、新たに保護フィルムを貼れば、きれいな液晶に戻るとのこと。

 

SONYのデジカメの液晶コーティング剥げに対処してみた | 鑑人

SONY製デジタルカメラRX100の液晶保護フィルムを張り替える | なたで日記

α7IIの液晶コーティング剥がれ : ZEISSレンズとかなんとか

 

実践

　とっくの昔に保証は切れていますし、自己責任で実践することにしました。まず図2の矢印で示すように、液晶画面端からカッターナイフの刃を入れ、保護層の端を少し剥がしました。

 

図2　カッターナイフを入れた箇所を矢印で示す

 

　その後、手で保護層を剥がしていきました。強く液晶画面本体に密着しているため、力のかけ方を誤り液晶画面のチルト機構を壊してしまわないよう、慎重に進めました。

　図3に剥がし終えた保護層を示します。液晶画面の写真は載せませんが、傷のない新品同様の姿が現れました。

　その後、市販のRX10M2用液晶保護フィルムを貼り付けました。液晶画面がきれいになり、まだまだ使えそうです、

 

図3　剥がし終えた保護層

 

おわりに

　汚いまま使い続けるしかないのかと思いましたが、剥がすことができました。ただ、数年でここまで劣化するくらいならデフォルトで貼らないでほしい気もしますが......

　真似するときはご自身の責任でお願いします。

MATLABでROS 2のカスタムメッセージを読み込む

MATLAB ROS 2

はじめに

　MATLABのROS Toolboxを使ってROS 2のrosbagを読み込むときに、独自定義のトピックを取り扱う方法のメモです。

実行環境

　この記事では、下記の環境を前提とします。ROS Toolboxは年々更新されているため、MATLABのバージョンは影響が大きいです。注意してください。

MATLAB用PC

OS：Windows 11
MATLAB：R2023b
Python：3.9.13 (Anacondaの仮想環境を使用)

ROS 2用PC

OS：Ubuntu 22.04 LTS
ROS 2：Humble

ステップ1：ROS ToolboxへPythonパスの登録

　公式ドキュメント[1]の通りに、ROS ToolboxへPython実行可能ファイルのパスを登録します。図1のように、Anacondaを用いて新たに作成した仮想環境"matlab_ros"を登録しましたが、問題なく動作しました。 (サポートされているかは確認していませんが...)



図1　Python実行可能ファイルのパス登録画面


ステップ2：カスタムメッセージのビルド

　ROS 2用PCからMATLAB用PCへ .msgファイルをコピーします。今回は下記のフォルダ構成としました。



図2　フォルダ構成

　次に、MATLABのコマンドラインにおいてros2genmsg関数を実行し、ビルドします。公式ドキュメント[2]によると、msgフォルダの親フォルダの親フォルダのパスを指定する必要があります。よって、図3の1行目のように、図2に示した最上位フォルダを指定してros2genmsg関数を実行します。

　ビルドに成功すると、図3の最終行のように「ビルドが成功しました」と表示されます。また、図4のようにmatlab_msg_genフォルダが生成されます。



図3　ros2genmsg関数実行時のコマンドライン



図4　ビルド後のフォルダ構成


ステップ3：読み取りスクリプトの作成

　ここで、図2に示した独自メッセージのうち、MotorPulse.msgを読み取るスクリプト (.mファイル) を作成します。MotorPulse.msgは、自作移動ロボットに備える左右のモータのエンコーダパルス数を格納するために作成したメッセージで、定義は下記の通りです。

std_msgs/Header header
int64 left_motor_pulse
int64 right_motor_pulse

　作成したスクリプトは下記の通りです。1行目でbagファイルのディレクトリ (mファイル実行時のカレントディレクトリからの相対パス) を指定します。'rosbag2_2024_12_08-14_43_17'フォルダの中にros2 bag record 実行時に作成された.yaml と .db3が配置されています。
　2行目で指定したbagファイルを読み込み、4行目で読み込んだbagファイルの記録開始時刻を取得します。5行目で自作の関数を用いて指定トピック (/motor_pulse_Data) のデータを取得し、構造体motor_pulse_Dataに格納します。7行目以降は、取得したデータを用いてグラフを作成します。

folder_path = 'ros2bag\rosbag2_2024_12_08-14_43_17';    % bagファイルのディレクトリを指定
bag_data = ros2bagreader(folder_path);                  % bagファイルを読み込み

start_time = bag_data.StartTime;                        % bagファイルの記録開始時刻を取得
motor_pulse_Data = read_MotorPulse(bag_data, '/motor_pulse_Data', start_time);  % 自作関数で指定トピックのデータを取得

% グラフを作成
plot(motor_pulse_Data.Time, motor_pulse_Data.left_motor_pulse)
hold on;
plot(motor_pulse_Data.Time, motor_pulse_Data.right_motor_pulse)
grid on;
legend(["左モータ", "右モータ"])
xlabel('時刻 [s]')
ylabel('エンコーダのパルス数')

% MotorPulse.msg形式のトピックを読み込む自作関数
function data = read_MotorPulse(bag_data, topic_name, start_time)
    % 指定したトピック名のメッセージを選択し、読み込む
    selectedBag = select(bag_data, 'Topic', topic_name);
    msgs = readMessages(selectedBag);
    
    % 構造体に格納する
    % メッセージのタイムスタンプ(sec + nanosec)を秒単位で計算し、記録開始時刻を基準に調整
    data.Time = double(arrayfun(@(i) msgs{i}.header.stamp.sec, 1:numel(msgs))') ...
        + double(arrayfun(@(i) msgs{i}.header.stamp.nanosec, 1:numel(msgs))') * 1e-9 - start_time;
    data.left_motor_pulse =  arrayfun(@(i) msgs{i}.left_motor_pulse, 1:numel(msgs))';   % left_motor_pulseを格納
    data.right_motor_pulse =  arrayfun(@(i) msgs{i}.right_motor_pulse, 1:numel(msgs))'; % right_motor_pulseを格納
end

　自作関数では、指定したトピック名のメッセージの読み込みと、構造体への格納を行います。ROS Toolboxで用意されているreadMessages関数を用いて、指定したトピック名のメッセージを20行目で読み込み、'msgs'に格納しています。しかし図5に示す通り、'msgs'は1サンプリングごとに作成された構造体が並んだセル配列となっており、扱いづらいです。
　そこで、24行目以降でフィールドごとに配列とし、構造体に格納しています。図6に作成した構造体を示します。



図5　msgsの中身



図6　構造体dataの中身



7~14行目で作成したグラフを、図7に示します。見慣れたグラフで落ち着きますね。



図7　作成したグラフ


おわりに

もっといい方法があったら教えてください。

参考文献

[1] ROS Toolbox システム要件
jp.mathworks.com

[2] rosgenmsg
jp.mathworks.com

Japanese Stable VLMをローカル環境で使ってみる

 

1. はじめに

Stability AIが2023年11月に発表した、画像に日本語でキャプショニングしてくれるJapanese Stable VLMをローカル環境で試してみました。

VRAM16GBでも一応動きました！ ja.stability.ai

 

2. PCのスペック

CPU：i5-13500

GPU：RTX4070TI SUPER (VRAM 16GB)

RAM：32GB

OS：ubuntu 22.04 LTS

 

3. 環境構築

3.1 ライブラリのインストール

transformers, accelerate, sentencepiece, protobuf, pillow, huggingface_hubをインストールしました。

 pip install transformers accelerate sentencepiece protobuf pillow huggingface_hub 

 

int8でモデルを読み込むために必要なbitstandbytesをインストールしました。

 pip install -i https://pypi.org/simple/ bitsandbytes 

 

3.2 作業フォルダの作成

図1のフォルダ構成としました。

python フォルダには、4章で作成するpythonコードを入れます。

pictures フォルダには、推論に用いる画像を入れます。

model フォルダには、3.3節でダウンロードするモデルを入れます。

図1　フォルダ構成

 

3.3 モデルのダウンロード

huggingfaceからモデルをダウンロードし、3.2節で作成したmodelフォルダに保存します。

今回はfp16のモデルをint8で読み込むので、model.fp16-0000x-of-00004.safetensorsをダウンロードします。model-0000x-of-00007.safetensorsはダウンロードしません。

他のサイズが小さいファイルは、どれが必要なのか考えるのが面倒だったので全てダウンロードしました。

huggingface.co

 

4. Pythonコード

公式の使用例とnpakaさんの記事を参考にpythonコードを作成し、3.2節で作成したpythonフォルダに、StableVLM_test.pyとして保存しました。

note.com

 

from transformers import AutoTokenizer, AutoModelForVision2Seq, AutoImageProcessor
from PIL import Image

# モデルとトークナイザーとプロセッサーの準備
model = AutoModelForVision2Seq.from_pretrained("/home/username/StableVLM/model",
 trust_remote_code=True, load_in_8bit=True, variant="fp16", max_memory='15GB', low_cpu_mem_usage=True)
tokenizer = AutoTokenizer.from_pretrained("/home/username/StableVLM/model")
processor = AutoImageProcessor.from_pretrained("/home/username/StableVLM/model")

# 入力画像の準備
image_path = "/home/username/StableVLM/pictures/" + input("画像.拡張子：")
image = Image.open(image_path).convert("RGB")

# プロンプトの準備
instructions = input("指示：")
inputs = input("入力：")

prompt = """
以下は、タスクを説明する指示と、文脈のある入力の組み合わせです。要求を適切に満たす応答を書きなさい。

### 指示: 
"""

prompt = prompt + instructions + "\n\n### 入力:\n" + inputs + "\n\n### 応答:\n"

#確認用にプロンプトをprint
print("\n-----プロンプトは下記です-----" + prompt + "-----プロンプト終わり-----\n") 

# 入力の準備
inputs = processor(images=image, return_tensors="pt")
text_encoding = tokenizer(prompt, add_special_tokens=False, return_tensors="pt")
inputs.update(text_encoding)

# 推論の実行
outputs = model.generate(
    **inputs.to(device=model.device),
    do_sample=False,
    num_beams=5,
    max_new_tokens=128,
    min_length=1,
    repetition_penalty=1.5,
)
generated_text = tokenizer.batch_decode(outputs, skip_special_tokens=True)[0].strip()
print(generated_text)

 

6, 7行目において、fp16のモデルを8bitで読み込むこと、メモリ使用量の最大値は15GBとすることを指定しています。

6, 8, 9, 12においてパスを指定しているので、環境に合わせて適宜書き換えてください。

 

5. 動作確認

5.1 使い方

Terminalを開き、4章で書いたコードを実行します。

 python ~/StableVLM/python/StableVLM_test.py 

 

推論に用いたい画像のファイル名を指定し、エンターキーを押します。

次に、プロンプトの指示を記入し、エンターキーを押します。

最後に、プロンプトの入力を記入し、エンターキーを押します。

プロンプトの応答は、指定しないことにしています。

5.2 使用例

5.2.1 使用例その1

図2に、実行時のTerminal画面例を示します。
画像のファイル名はtrack.jpg, プロンプトの指示は「画像を詳細に述べてください。」, プロンプトの入力はなしとしました。

図3にtrack.jpgを示します。

推論結果は「道路脇に緑色のトラックが停まっている」です。トラックは中央分離帯寄りの写真におり、実際は走行中と思われますが、大体あっているのでヨシ👈

 

図2　実行時のTerminal画面例

 

図3　track.jpg

 

VRAMの使用量は最大15GB程度で、推論にかかった時間は数秒でした。

なお、本記事中で与えた画像は、全てデジカメで撮影したものを1920x1280pxにリサイズした画像です。元の5472x3648pxのまま与えると、書いていないことを答える傾向にある気がしたため、リサイズしました。

 

5.2.2 使用例その2

画像の内容について質問することも可能です。

プロンプトの指示「与えられた画像を下に、質問に答えてください。」

プロンプトの入力「船の色は何色ですか。」

与えた画像は、図4に示すレインボーブリッジ遊歩道から撮影した東海汽船のジェットフォイルです。

推論結果「白とピンクです。」

正解ヨシ👈

図4　レインボーブリッジ遊歩道から撮影した東海汽船のジェットフォイル

 

5.2.3 使用例その3

プロンプトの指示「与えられた画像を下に、質問に答えてください。」

プロンプトの入力「何匹の鳥が写っていますか。」

与えた画像は、図5に示す洗足池で撮影したカルガモです。合計8匹ですね。

推論結果「5匹です。」

残念ながら不正解です。

 

図5　洗足池で撮影したカルガモ

 

6. おわりに

今回は、Japanese Stable VLMをVRAM16GBのローカル環境で試してみました。

触ってみた結果としては、一応それっぽい結果が出ないこともないという感じでした。

今後は、移動ロボットで撮影した画像を推論させ、遊びたいです（テキトー）

ミニPCをモバイルバッテリーからのUSB PD給電で使ってみた (自作移動ロボット用)

はじめに

　最近、図1に示す移動ロボットを自作して遊んでいます。UbuntuとROS 2の環境をミニPC上に構築し、LiDARやオドメトリ情報を入力してごにょごにょしてます。

　ミニPCへの電力供給源としてモバイルバッテリーを使ってみた結果、問題なく使えたかどうかお伝えします。移動ロボットを自作する方の参考になれば幸いです。（同様の構成を試して動かなくても責任は取らないです）

 

図1　自作移動ロボット

 

使用するPC

　minisforumのUN305Cを使用しています。スペックは下記です。ちなみにもう廃版のようです。図2に、UN305CのUSB Type-Cポートを示します。このポートは、USB PD給電を受けることができます。

　i3-N305は、ミニPCに最近よく使われているN100の上位っぽい製品です。i3と名前がついていますが、PコアはなくEコアのみ8個の構成です。消費電力が低く、なおかつそこそこ使えそうなので選びました。

 

CPU：intel i3-N305（8コア8スレッド）

GPU：内臓GPUのみ

RAM：16 GB

SSD：256 GB

OS：購入時のWindows11を削除し、Ubuntu 22.04 LTSをインストールし使用

 

※Ubuntu 22.04 LTSのインストール時、グラフィックドライバ周りのトラブルがあり、解決に時間を要しました。現在も、2つあるHDMIポートのうち片方が使えません。このPCにLinuxを入れるのはおすすめできません。
（公式非対応なのでMinisforumが悪いわけではありません）

 

図2　UN305CのUSB Type-C ポート

 

　なお、必要なUSB PD給電の出力は、ホームページに明記がありませんでした。参考として、付属のACアダプター出力は36 W（12 V、3 A）です。なお、最大33 W出力が可能なUSB PD充電器であるAnker 323 Chargerを使用すると、起動はできるものの高負荷時には落ちることがありました。

　カスタマーサポートに質問したところ、通常ならば65 W以上の出力が可能なUSB PD給電を用いると問題なく使えるとの返答がありました。

 

使用するモバイルバッテリー

　カスタマーサポートへの問い合わせ結果を受けて、65 W出力が可能なモバイルバッテリーであるAnker 537 Power Bankを選びました。大きいですが自作移動ロボットに入るサイズなのでヨシ👈

 

サイズ：約160 x 85 x 27 mm

出力：USB Type-C 単ポート使用時に最大65 W

容量：24000 mAh

 

使用テスト

テスト①　起動テスト

　まずは、最低限起動できることを確認しました。

　事前にUbuntu上の電源モードをバランスに設定してシャットダウンし、ACアダプタのケーブルを抜いてモバイルバッテリーを接続しました。電源ボタンを押したところ、正常に起動しました。

テスト②　高負荷テスト

　次に、高負荷時に落ちないことを確認しました。Ubuntu上の電源モードをパフォーマンスに設定した上で、Terminal上で下記のコマンドを打ち、8コア中6コアのCPU使用率が100 %となるように負荷 をかけました。その結果、落ちることなく正常に動作し続けました。

 stress -c 6 

　

テスト③　使用可能時間テスト

　最後に、何時間程度使用できるかを確認しました。Ubuntu上の電源モードをバランスに設定した上で、ミニPCに自作基板およびLiDARを接続しました。

※自作基板は、車輪の回転数制御、mems 9軸センサ値の読み取り等を行い、消費電力は1 W未満。LiDARは消費電力2 W程度。

　また、自作基板とLiDARそれぞれを制御するROS2 ノードを起動しました。このとき、CPU使用率は全コアが50 %程度でした。満充電状態のモバイルバッテリーを接続し、残量インジケータが3/4になるまでに、約3.5時間かかりました。

※残量が4つのLEDで表示されるので、バッテリー切れのぎりぎりまで使用することはできない。ぎりぎりを攻めたいなら、残量が液晶に数値で表示される機種を買おう。

 

　リチウムイオン電池の電圧を3.7 V、放電時の電力変換効率を80 %としたとき、今回のモバイルバッテリーの利用可能な電力量は約71 Whです。3.5時間でその3/4を消費したと仮定すると、平均消費電力は約15 Wであり、自作基板とLiDAR消費分を引くと、約12 Wです。

　intel i3-N305のTDPは15 Wであること、CPU使用率は約50 %であったこと、CPU以外にもRAM、SSD、冷却FAN等が電力を消費することを考えると、計算は合いますね。

 

おわりに

　今回は、自作移動ロボット用に買ったミニPCを、モバイルバッテリーからのUSB PD給電で動かしてみました。結果として無事に動き、CPU使用率50 %程度ならば3.5時間使用できました。

　みんなもミニPCを使ってロボットをつくろう！ いや、Jetsonかラズパイでよくね

MATLABを用いた小型ロケットのロール制御系設計

姿勢推定 姿勢制御 ロケット

1. はじめに

1.1 ご挨拶

本記事は、MATLAB/Simulink Advent Calendar 2023の12日目です。

東工大ロケットサークルCREATEが2022年11月に打ち上げました、小型ロケットC-59Jのロール制御系について紹介します。

MATLABを用いて設計したロール制御系について、主に次の3つの観点から記述しました。

  • 制御対象のモデル化とパラメータ推定
  • 制御ゲインの決定
  • 安定性評価

本記事中で取り上げたMATLABコードは、Githubにも上げていますのでご覧ください。

github.com

 

ロケットの機体構造については、ぜひこちらの記事をご覧ください。

tgkhtknk.hatenablog.com

 

1.2 背景

全国にはいくつもの学生ロケットサークルがあり、東京都大島町、秋田県能代市、和歌山県和歌山市などにて、共同打上実験を年に数回実施しています。

規模としましては、全長1~2m程度のロケットを、高度数百~数千mへ打ち上げています。

これまで、ロール制御 (機軸方向まわりの回転角制御) に挑戦したサークルは複数ありますが、制御系の設計法と制御結果について詳しく紹介した例は見当たりません。

ロケットの製作には半年～1年程度を要し、本番は1発勝負であるため、制御ゲインの試行錯誤的な調整ができない難しい環境にあります。

そこで本記事では、成功裡に終えたC-59Jのロール制御系に焦点を当てその詳細を紹介することで、今後ロール制御に挑戦する方々にとって有益な情報になればと思います。

さらに、MATLAB/Simunik界隈の皆様に向け、MATLABを使用して達成した成果を共有したいと思います。

 

2. ロール制御用ハードウェアの構成

図1に、小型ロケットC-59Jのうち、ロール制御に関連するハードウェアの模式図を示します。

ロールモーメントは、2枚の動翼が発生させる揚力により得ます。

2枚の動翼は、傘歯車を介して1個のMAXON社製エンコーダ付きギアモータにより駆動します。エンコーダには512pulse/countの2相インクリメンタルエンコーダを用い、ギアボックスのギア比は29.16です。

この構成により、四逓倍を用いることで出力軸の角度は約0.006度の分解能で計測されます。

 

MCUにはESP32を用います。

ピトー管により計測した対気速度、MEMS 9軸センサにより計測した機体系角速度、エンコーダにより計測した動翼角度などから、適切なモータ電圧指令値を生成し、モータドライバへPWM信号を送信します。

同時に、各センサ値の計測および計測値と制御値の保存を行います。

さらに、機体内から外の景色および動翼の動きを撮影し、ロール制御の成否を定性的に確認するために、2台の小型カメラを搭載します。

 

図1　ハードウェア構成

 

3. 制御対象および制御系のモデル化

3.1 概要

図2に制御対象および制御系を簡易に表したブロック線図を示します。

ただし、目標ロール角は、固定値が与えられるものと仮定します。

与えられた目標ロール角と、姿勢推定器が推定したロール角推定値、およびピトー管を用いて求めた対気速度推定値をもとに、目標動翼角度決定器が目標動翼角度を決定します。

 

次に、目標動翼角度と、エンコーダを用いて計測した動翼角度計測値から、動翼角度制御器がモータに電圧を印加します。

モータ・ギアボックス・傘歯車・動翼から構成されるモータ-動翼系は、印加された電圧に応じて回転します。

このとき、動翼角度および対気速度に応じて発生するロールモーメントが、機体のロール角を変化させます。

 

図2　全体ブロック線図

3.2 動翼角度制御のモデル化

3.2.1 モータ・動翼系のモデル化とシステム同定

図2において、ロール角のフィードバックループ内に、動翼角度のフィードバックループが存在します。まずは、この部分をモデル化してみましょう。

 

DCモータにおいて、電圧V (s) から角速度\dot\theta (s)までの伝達関数は、式(1)のように二次系で表せることが知られています。今回は、モータ-動翼系のモデル化にこの式を用いることとします。

\displaystyle \frac{\dot\theta \rm{(s)}}{V \rm{(s)}}=\frac{c}{s^2+as+b} 　(1)
 
ここで、  a, b, c はモータ-動翼系の機械的・電気的特性から決まる固定値です。
  a, b, c は、こちらの記事を参考にしたシステム同定実験により求めました。

sbasami-tech.hatenablog.com

 

図3に、システム同定実験における入力 (電圧) および出力 (角速度) の時間変化を示します。入力は正弦波とし、3 Hzから徐々に100 Hzまで周波数を上げています。

入力の周波数が上がるにつれ、出力の周波数が徐々に小さくなっていることが分かります。

 

図3　モータ-動翼系システム同定実験における入出力の時間変化

 

下記のMATLABコードを用いて、システム同定をしました。MATLABを使えば簡単だなあ...（中身を知らなすぎると危ないけど）

システム同定実験で得られた、1列目がduty比、2列目が角度計測値、3列目が前サンプリングとの時刻差であるcsvファイルを読み込んでいます。

 

図4に、同定実験における角速度の測定値 (図3の下段と同じ) 、およびシステム同定結果を用いたシミュレーション結果の角速度の時間変化を示します。（上記コードで得られるfigure(1)です。）

赤色の線は、システム同定実験における入力電圧(図3の上段)を、システム同定結果に基づくモデルに入力したときの応答をシミュレーションしたものです。

いい感じに同定できてそうですね。

  a=1462, b=53850, c=218100と求まりました。

 

図4　システム同定実験および同定結果を用いたシミュレーションの角速度

3.2.2 動翼角度制御器のモデル化

今回は、PD制御を用いて動翼の角度制御を行います。
比例ゲインと微分ゲインをそれぞれ  K_{Pm}, K_{Dm}とおきます。

簡単のために下記の仮定をおくと、動翼角度のフィードバックループは、図5のように表されます。

・動翼角度は誤差なく計測できる

・モータドライバの電圧制御は正確かつ時定数が小さく、モータ電圧指令値とモータ電圧は等しいとみなせる

 

図5　動翼角度フィードバック系のブロック線図


3.2.3伝達関数の導出とボード線図

図5の動翼角度フィードバック系について、伝達関数とボード線図を確認します。

開ループ伝達関数 G_{om}(s)は、式(2)で表されます。

\displaystyle G_{om}(s)=\frac{csK_{Dm}+cK_{Pm}}{s^3+as^2+bs}　(2)

一方、閉ループ伝達関数 G_{cm}(s)は、式(3)で表されます。

\displaystyle G_{cm}(s)=\frac{csK_{Dm}+cK_{Pm}}{s^3+as^2+(b+cK_{Dm})s+cK_{Pm}}　(3)

 

MATLABを使えば、簡単にボード線図が書けて、位相余裕とゲイン余裕も分かっちゃいます。ボード線図で位相余裕とゲイン余裕を確認しつつ、4章で示す時系列シミュレーションで応答を確認して、PDゲインを決めました。

上記のコードを実行すると、図6および図7が得られます。
 
まず図6の開ループ伝達関数を見てみましょう。
margin関数を用いると、ボード線図と同時にゲイン余裕と位相余裕も得られちゃいます。
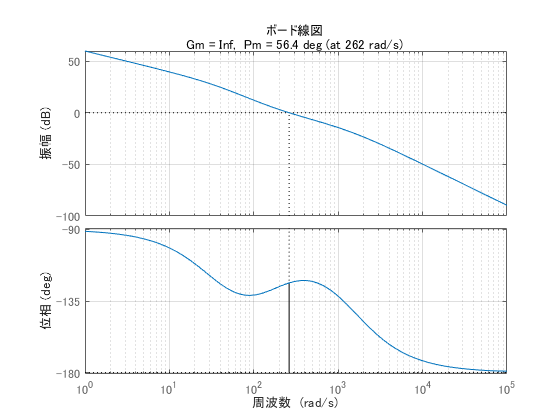
位相余裕は56.4度、位相が-180度以下にならないためにゲイン余裕は無限大となっています。
位相余裕、ゲイン余裕ともに充分でしょう。

図6　動翼角度フィードバック系の開ループ伝達関数のボード線図
 
次に、図7の閉ループ伝達関数を見てみましょう。
ある程度の周波数まで振幅・位相ともに0付近であり、その後どちらも下がっていく理想的な形ですね。
振幅が-3 dBになる周波数は395 rad/s ≒ 63 Hzです。このくらい高い周波数まで追従可能なら、安いPWMサーボモータを買うのではなく、MAXONモータを使って制御した意味があると言えるのではないでしょうか。

図7　動翼角度フィードバック系の閉ループ伝達関数のボード線図

3.3 全体のモデル化

3.3.1 機体系のモデル化とパラメータ推定

図2において機体系は、動翼角度と対気速度を入力、ロール角を出力としています。この部分をもう少し詳しく見てみましょう。なお、簡単のためにロール以外の他2軸の運動がロール運動へ与える影響は無視しています。

機体のロール軸まわりの主慣性モーメントを I [kgm^2]、動翼が発生させるモーメントをM [Nm]とおきます。このとき、簡単のために減衰項を無視すると、2つの関係は式(4)で表されます。

\displaystyle M=I\ddot{\phi}　(4)

これを伝達関数表現になおすと、式(5)となります。 Iの値は、CAD上の値を用いました。

もともとCREATEでは、ロケットの重量と重心を管理して設計するために、部品1つ1つの重量と位置を丁寧に登録しながら3D CAD上で機構設計をしていました。おかげで、慣性モーメントもすぐに求まり助かりました。

\displaystyle  \frac{\phi (s)}{M(s)}=\frac{1}{Is^2}　(5)

 

また、動翼角度\theta [rad/s]及び機軸方向の対気速度v [m/s]と、M [Nm]の関係は、複数の仮定の下で式(6)により表されます。ただし、Cは係数です。つまり、Mはvの二乗に比例し、\thetaに比例します。 

\displaystyle  M=Cv^2\theta　(6)

機軸方向以外の対気速度は無視でき、動翼角度=迎え角であるという仮定を置いています。また他の重要な仮定として、迎え角が小さく失速しないことがあります。失速するとMと\thetaの比例関係が成り立たなくなります。C-59Jでは動翼角度の範囲を±15 degと小さくしており、後述するCFD解析上でも失速は見られず仮定は成り立っていたと言えます。

係数CはCFD解析により求めました。CFD解析の詳細は、他メンバーが担当したため割愛します。

対気速度は20, 40, 60, 80 m/sの4段階、動翼角度は1, 3, 5, 7, 9, 11, 13, 15 degの8段階、計32通りの解析に最小二乗法を適用し、係数Cを算出しました。最小二乗法に用いたMatlabコードは下記です。

 

図8に動翼角度とロールモーメントの関係を示します。動翼角度が大きいときもCFD解析結果が近似結果の直線に乗っており、失速していないことが確認できます。

また、図9に対気速度とロールモーメントの関係を示します。こちらは、CFD解析結果が近似結果の二次曲線に乗っています。

図8　対気速度ごとの動翼角度とロールモーメントの関係。青丸でCFD解析結果、赤線で最小二乗法で求めた近似結果をそれぞれ示す。

 

図9　動翼角度ごとの対気速度とロールモーメントの関係。青丸でCFD解析結果、赤線で最小二乗法で求めた近似結果をそれぞれ示す。

 

3.3.2 目標動翼角度決定器のモデル化

目標動翼角度決定器は、ロール角推定値と目標ロール角及び対気速度推定値を入力とし、目標動翼角度を出力します。3.1節で示したように、後段の動翼角度制御器が、この目標値へ向けて動翼を制御します。

今回は、PD制御を用いて目標ロールモーメントM^r [Nm]を定め、式(6)に基づき係数Cと対気速度推定値\hat{v}の二乗で除算することで、目標動翼角度\theta^r [rad]を決定します。

対気速度がある値v_nであり、その推定値が\hat{v}_nであるときを考えると、ブロック線図は図10のように表されます。


図10　目標動翼角度決定器のブロック線図

3.3.3 伝達関数の導出とボード線図

簡単のために下記の仮定をおくと、図2のブロック線図は図11のように簡易化できます。

・ロール角は誤差なく計測できる

・対気速度は誤差なく計測できる

・対気速度はある値v_nで一定である

 

図11　簡易化した全体ブロック線図

このときの開ループ伝達関数 G_{oa}(s)を求めます。ロール角のフィードバックを除いて考えると、次の式が成り立ちます。

\displaystyle \phi(s)=(K_{Pa}+sK_{Da})\frac{1}{C{v_n}^2}G_{cm}(s)C{v_n}^2\frac{1}{Is^2}\phi^r(s)　(7)

式(3)、(7)より、開ループ伝達関数は次のように求まります。

\displaystyle G_{oa}(s)=\frac{\phi(s)}{\phi^r(s)}=\frac{cK_{Da}K_{Dm}s^2+c(K_{Pa}K_{Dm}+K_{Pm}K_{Da})s+cK_{Pa}K_{Pm}}{Is^5+aIs^4+(b+cK_{Dm})Is^3+cK_{Pm}Is^2}　(8)

 

次に、閉ループ伝達関数 G_{ca}(s)を求めます。ロール角のフィードバックを除かずに考えると、次の式が成り立ちます。

\displaystyle \phi(s)=(K_{Pa}+sK_{Da})\frac{1}{C{v_n}^2}G_{cm}(s)C{v_n}^2\frac{1}{Is^2}(\phi^r(s)-\phi(s))　(9)

式(3)、(9)より、閉ループ伝達関数は次のように求まります。

\displaystyle G_{ca}(s)=\frac{\phi(s)}{\phi^r(s)}\\= \frac{cK_{Da}K_{Dm}s^2+c(K_{Pa}K_{Dm}+K_{Pm}K_{Da})s+cK_{Pa}K_{Pm}}{Is^5+aIs^4+(b+cK_{Dm})Is^3+c(K_{Pm}I+K_{Da}K_{Dm})s^2+c(K_{Pa}K_{Dm}+K_{Pm}K_{Da})s+cK_{Pa}K_{Pm}}　(10)

 

3.2.3節と同様にMATLABを用いてボード線図を書きます。下記のコードを実行すると、図12および図13が得られます。

図12の開ループのボード線図を見ると、位相余裕は52.8度、ゲイン余裕は34.3 dBです。今回は目標ロール角一定の定値制御であることもあり、余裕はより小さくとも問題ないとも考えられます。しかし、4.3節に後述するように対気速度推定値の精度に不安があること、ここまでのモデル化で複数の仮定を用いた簡易化を行っておりそれが妥当であるか不安があること、本番一発勝負なのでぎりぎりを攻めたくないことから余裕は大きくとることとしました。

図13の閉ループのボード線図を見ると、振幅が-3 dBになる周波数は22.4 rad/s ≒ 3.6 Hzです。ロール制御が可能な時間は7秒間程度あるので、十分な制御帯域と言えます。

図12　系全体の開ループ伝達関数のボード線図

 

図13　系全体の閉ループ伝達関数のボード線図

 

4. シミュレーションと事前調整

4.1 動翼角度制御のシミュレーション

ここまでボード線図上で安定性を確認してきましたが、次は時系列シミュレーション上で確認します。まず、動翼角度制御のシミュレーションを行います。

式(1)及び \theta\rm{(s)}=\frac{1}{\rm{s}}\dot\thetaより、式(11)が得られます。ラプラス逆変換を用いると、時間領域では式(12)のように書けます。

\displaystyle \frac{\theta \rm{(s)}}{V \rm{(s)}}=\frac{c}{s^3+as^2+bs} 　(11)

\displaystyle \dddot\theta(t)=cV(t)-a\ddot\theta(t)-b\dot\theta(t) 　(12)

PD制御を用いてモータ電圧Vを決め、式(12)を用いて\dddot\thetaを更新し、オイラー法の積分を用いて\ddot\theta、\dot\theta、\thetaを更新するシミュレーションコードが下記です。

シミュレーション周期は10000 Hz、制御周期は500 Hzとしています。また電源電圧を10 Vに設定し、±10 V以上のモータ電圧とならないよう制限をほどこしています。

図14にシミュレーション結果を示します。すばやく目標値へ収束していることが分かります。また、伝達関数では表現されていない電圧の上下限があっても、問題なく制御できていることが確認できます。

図14　動翼角度制御シミュレーション結果。上段にモータ電圧、下段に目標動翼角度及び動翼角度を示す。

 

本記事では詳細を割愛しますが、飛行中に動翼が受ける空力がうむ、動翼を回転させるモーメントによって発生する動翼角度偏差が十分に小さいことも、シミュレーションにより確認しました。

 

4.2 ロール制御のシミュレーション

次に、4.1節の動翼角度制御シミュレーションを組み込んだ、ロール制御全体のシミュレーションを行います。

図10のブロック線図のように目標動翼角度を定め、その目標値へ向けて4.1節と同様に動翼角度を制御し、得られた動翼角度と式(4)を用いてロール角加速度\ddot\phiを更新し、オイラー法の積分により\dot\phi、\phiを更新するシミュレーションコードが下記です。

シミュレーション周期と制御周期は4.1節と同様としています。また、目標動翼角度を±14度に制限しています。

 

図15にシミュレーション結果を示します。約0.5秒で目標ロール角付近に収束しており、問題なく制御できていることが確認できます。

図15　ロール制御シミュレーション結果。上段に目標ロール角及びロール角、中段に目標動翼角度及び動翼角度、下段にモータ電圧を示す。

 

4.3 初期値及び誤差の考慮

4.2節で実施したシミュレーションは、制御開始時のロール角速度がゼロであったり、制御に用いる状態量は真値を使用していたりと、理想的な条件となっています。

本記事ではその結果は示しませんが、4.2節のコードを改良して下記の要素入れたシミュレーションを実施し、その場合でも目標ロール角へ収束することを確認しています。

① 大きな初期ロール角速度を持つ

② 固定翼のミスアラインメント等に起因する外乱ロールモーメントが存在する

③ ギアのバックラッシに起因する動翼角度計測誤差が存在する

④ ロール角速度の計測に遅れが存在する

⑤ 大きな対気速度計測誤差が存在する

 

5章で後述するように、実機では飛翔の途中でロール制御を開始しています。外乱ロールモーメントの状況しだいでは、制御開始時に大きなロール角速度を持っているため、その場合でも問題ないことを①で確認しました。

②では、CREATEの過去機体データを参考に、式(4)の左辺に外乱ロールモーメントを正弦波の形で付加し確認しました。

③では、ギアのカタログに記載があるバックラッシ値を用い、式(6)における動翼角度と動翼角度制御器が用いる動翼角度に差を設けて確認しました。

MEMSセンサMPU9250の角速度出力にローパスフィルタを設定していました。さらに、そのセンサ値からロール角速度を計算した後に、ローパスフィルタを施しました。これらによる遅れを考慮し④では、真のロール角速度及びロール角と、目標動翼角度決定器が用いる値に差を設けて確認しました。

⑤が最も大きな問題でした。ピトー管の信頼性が低くかったため、対気速度推定値と真値が最大1.5倍ずれていても安定となることを確認しました。具体的には、式(7)において分母と分子に登場し打ち消しあっている{v_n}^2が異なる値である場合の式(8)を作成し、ゲイン余裕と位相余裕を確保できていることを確かめました。また、時系列シミュレーションでも同様の確認を行いました。

 

5. ロール制御実験

5.1 実験条件

5.1.1 飛行プロファイル

ここまで、事前のロール制御系設計について紹介しました。5章では、実際に打ち上げた際の結果を紹介します。

図16に飛行プロファイルを示します。横軸は離床を基準とした時刻、縦軸は気圧センサのデータから算出した高度です。

C-59Jは、エンジン燃焼開始の直後に離床し、離床後約2.7秒で燃焼終了しました。

その後は約7秒間の弾道飛行の後、最高高度の約1秒後にパラシュートを開放し、減速落下しました。

 

安全性に配慮した自主的な規制により、ロール制御はエンジン燃焼終了後に開始することとしました。また、パラシュート開放後は大きな対気速度が得られず、動翼がロールモーメントを発揮できないため、ロール制御が成り立ちません。

よって、ロール制御は弾道飛行中にのみ、約7秒間実施しました。

 

図16　飛行プロファイル

5.1.2 パラメータ設定

動翼角度制御における制御ゲインは、  K_{Pm}=240, K_{Dm}=1.5 とし、

目標動翼角度決定器における制御ゲインは  K_{Pa}=0.8, K_{Da}=0.07 としました。

 

また、ESP32への実装にあたっては、ノイズの影響を低減するため、制御に用いる計測値の一部にデジタルローパスフィルタを施しました。

ピトー管から算出した対気速度には、カットオフ周波数20 Hzの1次のデジタルローパスフィルタを施しました。

MEMS角速度センサから算出したロール角速度には、カットオフ周波数50 Hzの1次のデジタルローパスフィルタを施しました。

 

5.1.3 初期値

ロール制御開始時において、ロール角は125.5 deg、ロール角速度は-69.45 deg/sでした。

 

5.2 実験結果

5.2.1 動画による確認

実験結果を、まずは動画で定性的に確認しましょう。

右側が機体に搭載した小型カメラを用いて撮影した映像です。映っている黒い板が動翼です。

中央上が、MEMSジャイロセンサを用いて計測した機体姿勢を、CGで再現した映像です。中央下が、ロール角のグラフです。

左側上が、エンコーダで計測した動翼角度を、CGで再現した映像です。左側下が動翼角度のグラフです。

 

離床すると、C-59Jはロールしています。これは、機体後端にある固定翼のミスアラインメント、ノーズ形状の非対称性等により発生した、外乱ロールモーメントの影響と考えられます。

離床の約2.7秒後にロール制御が開始され、動翼が動き始めます。その後すぐに、ロールがほぼ停止していることが分かりますね！

 

5.2.2 計測データによる確認

図17に、ロール角の時間変化を示します。

青色で示したロール制御開始前は、ロール角が変化していることが分かります。

一方、ロール制御開始後は、素早く目標ロール角に収束しています。

図17　ロール角の時間変化。ロール制御開始前を青色、開始後を赤色で示す。

 

図18に、ロール制御開始直後の、ロール角の時間変化を示します。

整定時のロール角を90度とみなすと、整定時間 (95%) はたったの0.27秒でした！

 

図18　ロール制御開始直後におけるロール角の時間変化

 

図19に、ロール制御開始からパラシュート開放付近までの、ロール角の時間変化を示します。

制御開始直後を除き、目標ロール角からの偏差が±4度以内に抑えられていることが分かります。

図19　ロール制御開始からパラシュート開放付近までのロール角の時間変化

 

図20に、動翼角度および目標動翼角度の時間変化を示します。
動翼角度は目標値に精度よく追従していることが分かります。

モータ軸に取り付けたエンコーダで計測しているので、ギアボックスおよび傘歯車のバックラッシが計測できない誤差として存在はしていますが。

図20　動翼角度および目標動翼角度の時間変化。動翼角度は、ロール制御開始前を青　
色、開始後を赤色で示す。目標動翼角度は黒色で示す。

 

6. おわりに

皆さんもぜひ、挑戦してみてください。打ち上げ本番は胃がキリキリして楽しいです!